讨论一个数学问题
- kcupida为区间A内的一个数,对于任意a做倒数运算得到b,b为区间B的元素。任意b的倒数a',都能在A的区间内找到,且a’=a,则A等势于B,这个有问题吗?
- yyyymm84
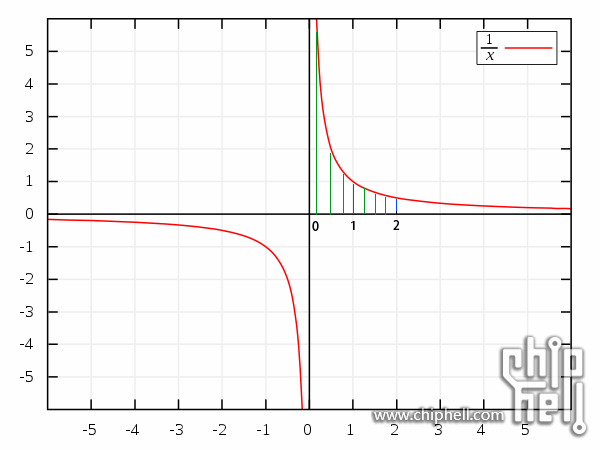
y=1/x,在0-1范围内的曲线上的点,投影到x轴与x轴0-1上的点,建立一一对应关系。
y=1/x,在1-2范围内的曲线上的点,投影到x轴与x轴0-2上的点,建立一一对应关系。
倒数数量对应原数数量可一一对应,既然原数数量相同,那么倒数数量相同。 - kcupid只讨论数量,不讨论大小
- kcupidy=1/x是关于y=x的对称,应该是0,1与1-正无穷关于(1.1)对称
- kcupid很棒,帮我回复一下61楼

- neil_aug
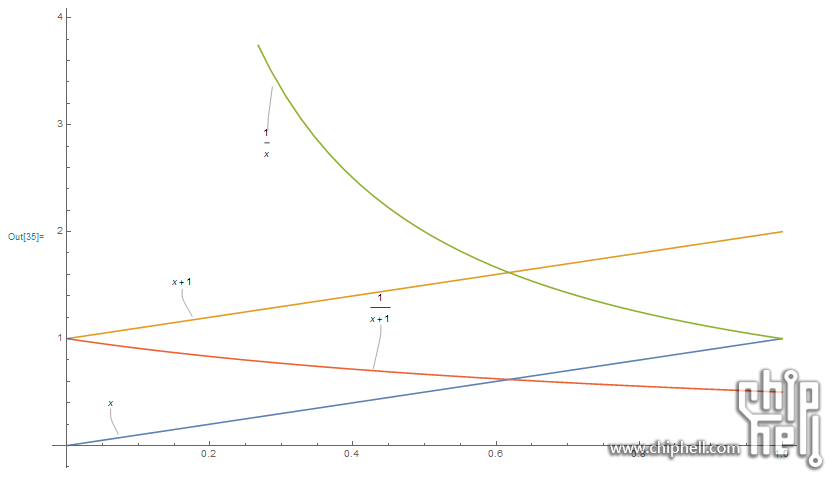
一目了然 - neil_aug就你的集合来说
A=x,B=x+1
A元素的倒数可能超出B集合。比如0.4的倒数是2.5并不在B集合内,两个势怎么相等? - neil_aug看107的图,x,x+1很明显在y轴的投影是一样长,它们是相等的。
1/x的投影范围最大,1/1+x的投影范围最小。1/1+x与x也并不等势。你的一一对应哪来的? - yx先谢郭嘉所以A~B~C~D了(等势or对等)
虽然它们不一样长,但是里面的元素数量相等啊,和实数集一样多(不可数,所以你也没必要数)
一一对应或对等可用于比较集合的大小(即集合所含元素个数的比较)。空集只与自身对等;两个有限集对等当且仅当它们的元素个数相同;与自然数集对等的集合称为可列集或可数集,与实数集对等的集合称为具有连续势,它们四个就是。 - QuaintJadeLZ跑上来就搞实数集(势为ℵ1)太勉强了,建议先从可列集(势为ℵ0)入门。
不要以有限集合的思维去理解无限集合。比方说,以下集合的元素个数是一样多的:
* 所有自然数
* 所有整数
* 所有偶数
* 所有有理数
* [0,1]区间内的有理数
如果你无法理解的话,说明集合论不适合你,建议不要再纠结了。 - QuaintJade这当然是错误的。
你面对的是无限集合,所以你不能想当然地套用有限集合的任何思维。
无限集合B是无限集合A的一个子集 (A≠B),然而B的元素数量可以与A的元素数量一样多。 - coconutgallo楼主有兴趣可以看看测度论或者实变函数/泛函分析。先说结论:这两个数量是一样的,数学上叫等势(因为两个无穷的集合可能数量不相等,比如所有整数(这种无穷叫可数)和全体实数(不可数))。
另外我们可以证明零一实数区间和负无穷到正无穷等势(数量相等),思路就是你说的构造一个(双射)函数使得两边元素一一对应。在0-1和1-2的例子里很简单,就是y=x+1就够了。 - lujj6688一样多的,兄得,f(x)=1/x, x \in (0,1) , 就是一个(0,1)到(1, +\infinity)的一个双射(单射,满射)。
维基百科-单射,双射和满射
康托尔-伯恩斯坦-施罗德定理
等势中文等势的定义不全,等势也可以用到无限集合:The definition of equinumerosity using bijections can be applied to both finite and infinite sets and allows one to state whether two sets have the same size even if they are infinite。
再给你举个你会觉得不一样多的例子,全体偶数的集合和自然数的集合是等势的,说明偶数的集合的元素数量和自然数集合的元素数量是一样的。 - kcupid请回答一下109楼的疑问
- lujj6688我为啥要回答他的问题?他那样的讨论方法本来就是不对的。你不要转移话题。定理定义都已经给你了。
- Celia一样多……每一个数字+1对应下一个区间的数,并不会找不到对应不到的数
- 独眼豆豆关键时刻LZ还是用运算后数字的大小和运算次数的多少混淆了概念。。。
- lyboo加法运算是数运算, 等号两侧的数值定义相同, 所以A + 1 = B做数量比较是有意的
导数运算是变化率运算, 等号两侧的数值定义不同, 所以f(A) = B做数量比较是无意的
当你对(1~2)或者(0~1)的数值求导的时候, 求导后数值定义已经发生改变, 两者只存在映射关系, 不存在对等关系 - gengzp楼主错把个数和区间划等号了。
- assea无穷不能和无穷比大小,初中知识
- 微‖吾存在双射是判断条件。楼主构造的函数不满足双射,不等于不存在这样的双射,如x=>x+1
- tmdodd无穷之间的运算不是这样的
- wwwinsky你所犯的错误,都是基于这一句。
- Taylor77取倒数这个行为不可取,改变了取极限的条件。
应该求证的的东西是,在这两个区间,取同样增量的积分大小是否相同,这个积分就是他们的长度,都是1,所以这两个极限的比值也是1,所以他们是等价极限,故题设成立。